La lógica proposicional es la parte de la lógica que estudia la formación de proposiciones complejas a partir de proposiciones simples, y la inferencia de proposiciones a partir de proposiciones, pero sin tener en cuenta la estructura interna de las proposiciones más simples.
Una lógica proposicional es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.
La lógica proposicional es la más antigua y simple de las formas de lógica. Utilizando una representación primitiva del lenguaje, permite representar y manipular aserciones sobre el mundo que nos rodea. La lógica proposicional permite el razonamiento, a través de un mecanismo que primero evalúa sentencias simples y luego sentencias complejas, formadas mediante el uso de conectivos proposicionales, por ejemplo Y (AND), O (OR). Este mecanismo determina la veracidad de una sentencia compleja, analizando los valores de veracidad asignados a las sentencias simples que la conforman.
Considérese el siguiente argumento:
Mañana es miércoles o mañana es jueves.
Mañana es miercoles
Por lo tanto, mañana es miércoles.
Está soleado o está nublado.
No está nublado.
Por lo tanto, está soleado.
Ni está soleado ni está nublado.
No está nublado.
Por lo tanto, está soleado.
p o q
No q
Por lo tanto, p
Ni p ni q
No q
Por lo tanto, p
Una lógica proposicional es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.
La lógica proposicional es la más antigua y simple de las formas de lógica. Utilizando una representación primitiva del lenguaje, permite representar y manipular aserciones sobre el mundo que nos rodea. La lógica proposicional permite el razonamiento, a través de un mecanismo que primero evalúa sentencias simples y luego sentencias complejas, formadas mediante el uso de conectivos proposicionales, por ejemplo Y (AND), O (OR). Este mecanismo determina la veracidad de una sentencia compleja, analizando los valores de veracidad asignados a las sentencias simples que la conforman.
Considérese el siguiente argumento:
Mañana es miércoles o mañana es jueves.
Mañana es miercoles
Por lo tanto, mañana es miércoles.
Está soleado o está nublado.
No está nublado.
Por lo tanto, está soleado.
Ni está soleado ni está nublado.
No está nublado.
Por lo tanto, está soleado.
p o q
No q
Por lo tanto, p
Ni p ni q
No q
Por lo tanto, p
NOMBRE
|
CONECTOR
|
SÍMBOLO
|
| Conjunción Disyunción Negación Implicación Equivalencia |
AND
OR
NOT
If-Then
Igual
|
^
v
~
=>
=
|
| Conectiva | Expresión en el lenguaje natural | Ejemplo | Símbolo en este artículo | Símbolos alternativos |
|---|---|---|---|---|
| Negación | no | No está lloviendo. |  | 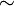 |
| Conjunción | y | Está lloviendo y está nublado. |  | 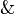  |
| Disyunción | o | Está lloviendo o está soleado. |  | |
| Condicional material | si... entonces | Si está soleado, entonces es de día. |  |  |
| Bicondicional | si y sólo si | Está nublado si y sólo si hay nubes visibles. |  |  |
| Negación conjunta | ni... ni | Ni está soleado ni está nublado. | 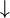 | |
| Disyunción excluyente | o bien... o bien | O bien está soleado, o bien está nublado. | 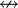 | 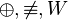 |
- Es un argumento válido. Quiere decir que es imposible que las premisas sean verdaderas y la conclusión falsa. Esto no quiere decir que la conclusión sea verdadera. Si las premisas son falsas, entonces la conclusión también podría serlo. Pero si las premisas son verdaderas, entonces la conclusión también lo es. La validez de este argumento no se debe al significado de las expresiones «mañana es miércoles» y «mañana es jueves», porque éstas podrían cambiarse por otras y el argumento permanecer válido. Por ejemplo:
Las expresiones de las que depende la validez de los argumentos se llaman constantes lógicas. La lógica proposicional estudia el comportamiento de algunas de estas expresiones, llamadasconectivas lógicas. En cuanto a las expresiones como "está nublado" o "mañana es jueves", lo único que importa de ellas es que tengan un valor de verdad. Es por esto que se las reemplaza por simples letras, cuya intención es simbolizar una expresión con valor de verdad cualquiera. A estas letras se las llama variables proposicionales, y en general se toman del alfabeto latino, empezando por la letra p, luego q, r, s, etc. Así, los dos primeros argumentos de esta sección podrían reescribirse así:
Y el tercer argumento, a pesar de no ser válido, puede reescribirse así:
La principal debilidad de la lógica proposicional es su limitada habilidad para expresar conocimiento. Existen varias sentencias complejas que pierden mucho de su significado cuando se las representa en lógica proposicional. Por esto se desarrolló una forma lógica más general, capaz de representar todos los detalles expresados en las sentencias, esta es la lógica de predicados.
La lógica de predicados está basada en la idea de las sentencias realmente expresan relaciones entre objetos, así como también cualidades y atributos de tales objetos. Los objetos pueden ser personas, objetos físicos, o conceptos. Tales cualidades,relaciones o atributos, se denominan predicados. Los objetos se conocen como argumentos o términos del predicado.
Al igual que las proposiciones, los predicados tienen un valor de veracidad, pero a diferencia de las preposiciones, su valor de veracidad, depende de sus términos. Es decir, un predicado puede ser verdadero para un conjunto de términos, pero falso para otro.
A continuación se dan algunos ejemplos de predicados cuantificados:
" X, [niño (X) => le_gusta (X, helados)].
" Y, [mamífero (Y) => nace (Y, vivo)].
$ Z, [cartero(Z) ^ mordió (boby, Z)].
l cuantificador existencial es más difícil de reemplazar. El cuantificador existencial garantiza la existencia de uno o más valores particulares (instancias) de la variable cuantificada, que hace a la cláusula verdadera. Si se asume que existe una función capaz de determinar los valores de la variable que hace la cláusula verdadera, entonces simplemente se remueve el cuantificador existencial y se reemplaza las variables por la función que retorna dichos valores. Para la resolución de problemas reales, esta función, llamada función de Skolem, debe ser conocida y definida.
Unificación
Cuando se tienen sentencias compuestas por predicados y conectivos lógicos, se debe evaluar la veracidad de cada uno de sus componentes para determinar si toda la sentencia es verdadera o falsa. Para ello, se busca en el conjunto de axiomas la forma de establecer la veracidad de los predicados componentes. Un predicado componente se dice que es verdadero si se identifica con un axioma de la base de información. En la lógica de predicados, este proceso es algo complicado ya que las sentencias pueden tener términos variables. A los predicados que tienen variables por argumentos, se los denomina patrones.
La unificación es el proceso de computar las sustituciones apropiadas que permitan determinar si dos expresiones lógicas, ya sean predicados o patrones, coinciden.
El proceso de unificación involucra los siguientes pasos:
- Todo predicado que no contenga variables en sus argumentos, deben tener un axioma que se identifique totalmente, para considerarlo como verdadero.
- Si un predicado contiene una variable, esta debe ser asociada a un valor determinado. Esta asociación se realiza buscando en la base de axiomas y seleccionando todos aquellos que se identifican con el patrón en todo, excepto por la variable. La variable es asociada con el valor en la posición correspondiente del axioma. Si más de un axioma se identifica con el predicado dado, todos los valores asociados son considerados y son tratados separadamente.
- El proceso de identificación continua asumiendo que el valor de la variable es el valor asociado, en cualquier lugar que esta aparezca.
- Los conectivos lógicos son aplicados a todos los predicados, para determinar la veracidad de la sentencia dada.
El proceso de razonamiento, por lo tanto, involucra la realización de inferencias, a partir de hechos conocidos. Realizar inferencias significa derivar nuevos hechos a partir de un conjunto de hechos conocidos como verdaderos. La lógica de predicados proporciona un grupo de reglas sólidas, con las cuales se pueden realizar inferencias.
Ventajas y desventajas de la Lógica de Predicados
A continuación se presentan algunos aspectos característicos de la lógica de predicados y su implementación computacional, el lenguaje de prograRazonamiento Progresivo...
- Unificación (Matching).- En este paso, en las reglas en la base de conocimientos se prueban los hechos conocidos al momento para ver cuáles son las que resulten satisfechas. Para decir que una regla ha sido satisfecha, se requiere que todas las premisas o antecedentes de la regla resuelvan a verdadero.
- Resolución de Conflictos.- Es posible que en la fase de unificación resulten satisfechas varias reglas. La resolución de conflictos involucra la selección de la regla que tenga la más alta prioridad de entre el conjunto de reglas que han sido satisfechas.
- Ejecución.- El último paso en la interpretación de reglas es la ejecución de la regla. La ejecución puede dar lugar a uno o dos resultados posibles: nuevo hecho (o hechos) pueden ser derivados y añadidos a la base de hechos, o una nueva regla (o reglas) pueden ser añadidas al conjunto de reglas (base de conocimiento) que el sistema considera para ejecución.
Un conjunto de aplicaciones adecuadas al razonamiento progresivo incluye supervisión y diagnóstico en sistemas de control de procesos en tiempo real, donde los datos están continuamente siendo adquiridos, modificados y actualizados. Estas aplicaciones tienen 2 importantes características:
- Necesidad de respuesta rápida a los cambios en los datos de entrada.
- Existencia de pocas relaciones predeterminadas entre los datos de entrada y las conclusiones derivadas.
Manejo de incertidumbre.- Una de las mayores desventajas de la lógica de predicados es que sólo dispone de dos niveles de veracidad: verdadero y falso. Esto se debe a que la deducción siempre garantiza que la inferencia es absolutamente verdadera. Sin embargo, en la vida real no todo es blanco y negro. En cierta forma el PROLOG ha logrado mitigar esta desventaja, permitiendo la inclusión de factores de certeza.
Razonamiento monotónico.- La lógica de predicados al ser un formalismo de razonamiento monotónico, no resulta muy adecuada para ciertos dominios del mundo real, en los cuales las verdades pueden cambiar con el paso del tiempo. El PROLOG compensa esta deficiencia, proporcionando un mecanismo para remover los hechos de la base de datos. Por ejemplo, en TURBO PROLOG se tiene la cláusula retractall.
Programación declarativa.- La lógica de predicados, tal como está diseñada en PROLOG, es un lenguaje de programación declarativo, en donde el programador sólo necesita preocuparse del conocimiento expresado en términos del operador de implicación y los axiomas. El mecanismo deductivo de la lógica de predicados llega a una respuesta (si esto es factible), utilizando un proceso exhaustivo de unificación y búsqueda. A pesar que la búsqueda exhaustiva puede ser apropiada en muchos problemas, también puede introducir ineficiencias durante la ejecución. Para lograr un cierto control en el proceso de búsqueda, PROLOG ofrece la operación de corte, CUT. Cuando no se utiliza el CUT, PROLOG se convierte en un lenguaje puramente declarativo.
El Proceso de Razonamiento
El proceso de razonamiento en un sistema basado en reglas es una progresión desde un conjunto inicial de afirmaciones y reglas hacia una solución, respuesta o conclusión. Como se llega a obtener el resultado, sin embargo, puede variar significativamente:
- Se puede partir considerando todos los datos conocidos y luego ir progresivamente avanzando hacia la solución. Este proceso se lo denomina guiado por los datos o de encadenamiento progresivo (forward chainning).
- Se puede seleccionar una posible solución y tratar de probar su validez buscando evidencia que la apoye. Este proceso se denomina guiado por el objetivo o de encadenamiento regresivo
 Razonamiento Progresivo...
Razonamiento Progresivo...- Unificación (Matching).- En este paso, en las reglas en la base de conocimientos se prueban los hechos conocidos al momento para ver cuáles son las que resulten satisfechas. Para decir que una regla ha sido satisfecha, se requiere que todas las premisas o antecedentes de la regla resuelvan a verdadero.
- Resolución de Conflictos.- Es posible que en la fase de unificación resulten satisfechas varias reglas. La resolución de conflictos involucra la selección de la regla que tenga la más alta prioridad de entre el conjunto de reglas que han sido satisfechas.
- Ejecución.- El último paso en la interpretación de reglas es la ejecución de la regla. La ejecución puede dar lugar a uno o dos resultados posibles: nuevo hecho (o hechos) pueden ser derivados y añadidos a la base de hechos, o una nueva regla (o reglas) pueden ser añadidas al conjunto de reglas (base de conocimiento) que el sistema considera para ejecución.
En esta forma, la ejecución de las reglas procede de una manera progresiva (hacia adelante) hacia los objetivos finales.Un conjunto de aplicaciones adecuadas al razonamiento progresivo incluye supervisión y diagnóstico en sistemas de control de procesos en tiempo real, donde los datos están continuamente siendo adquiridos, modificados y actualizados. Estas aplicaciones tienen 2 importantes características:- Necesidad de respuesta rápida a los cambios en los datos de entrada.
- Existencia de pocas relaciones predeterminadas entre los datos de entrada y las conclusiones derivadas.
Otro conjunto de aplicaciones adecuadas para el razonamiento progresivo está formado por: diseño, planeamiento y calendarización, donde ocurre la síntesis de nuevos hechos basados en las conclusiones de las reglas. En estas aplicaciones hay potencialmente muchas soluciones que pueden ser derivadas de los datos de entrada. Debido a que estas soluciones no pueden ser enumeradas, las reglas expresan conocimiento como patrones generales y las conexiones precisas entre estas reglas no pueden ser predeterminadas.
.jpg)

.jpg)
No hay comentarios:
Publicar un comentario